Basics of Graph
Graph theory is a mathematical discipline that studies the properties and relationships of graphs, which consist of nodes (vertices) connected by edges, enabling analysis of various real-world systems and phenomena.
Goals
By the end of this lesson, you should be able to:
- Use Dictionary and OOP to represent graph
- Define graph, vertices, edges and weights
- Differentiate directed and undirected graphs
- Define paths
- Create a
Vertexclass and a Graph class - Represent graphs using adjacency-list representation or adjacency-matrix representation
- Extend class Vertex and Graph for graph traversal algorithm
graph,adjacency matrix,adjacency list,vertex,neighbours,edge,weight,directional edge
What is a Graph?
In previous sections, we have worked with various algorithms and data. For example, we did sorting algorithm in a sequence of data of a list or array-like type. List and array is one kind of data where the item has relationship only with its previous and next item in a sequence. Stack and Queues are another kind of data structures. Even with these two, each item is related only in linear fashion, either with the next one at the top of the Stack or with the next in the sequence of the Queue. A Graph allows more relationship to be represented between each item. Two examples of graph data structures are shown below.
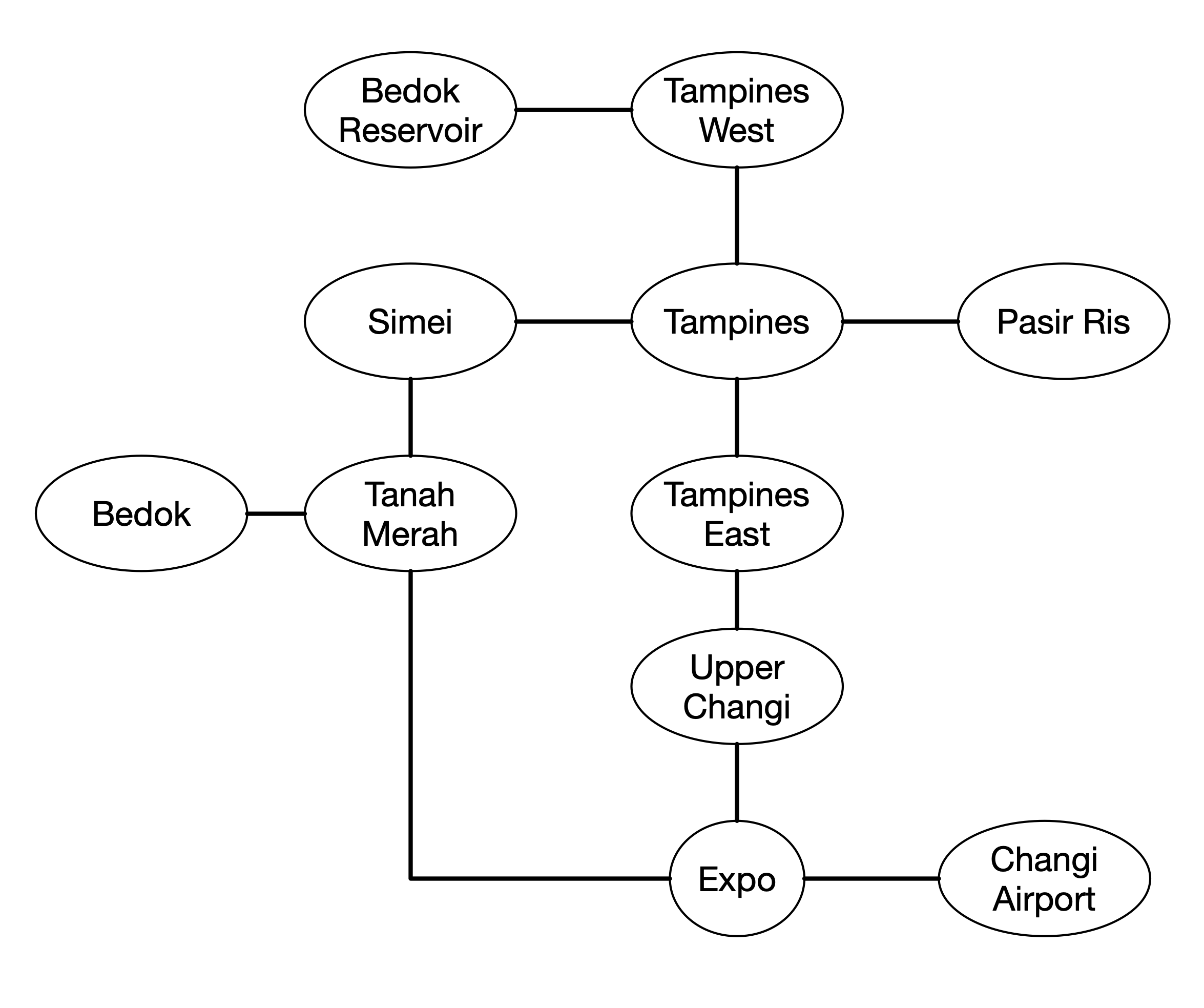

In the first example, the graph represent a kind of connection between places like in a map. With this kind of data, we can find a path from one place to another place or finding the shortest distance between two places. In the second example, the graph represent the control flow of a computer program. Compiler can use this information to optimize the code. Both are a Graph data type that represent different things. We can define a few things when dealing with a Graph.
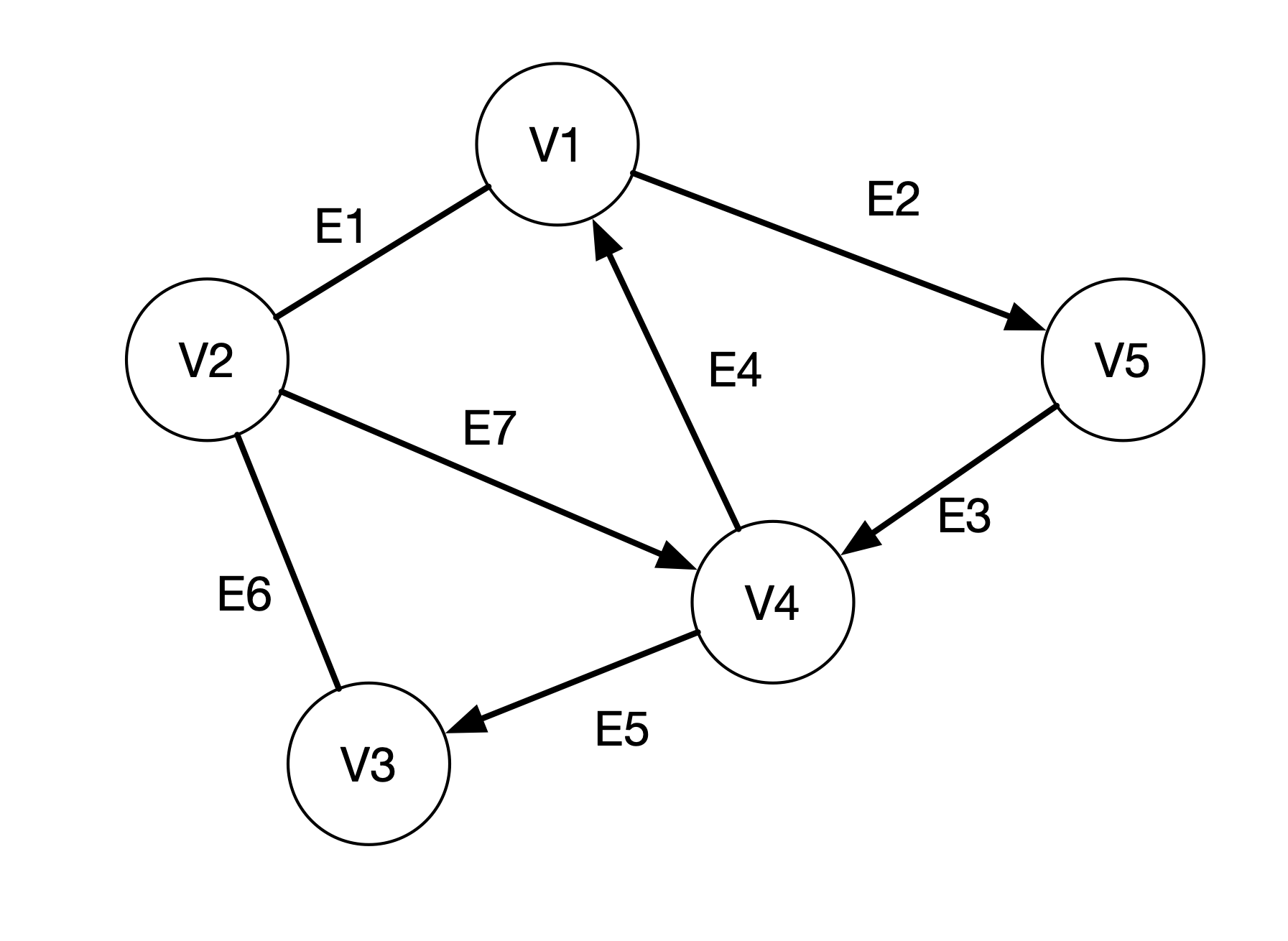
- Vertex: A vertex is a node that is connected by edges in a graph. A vertex can have a name which is also called its "key". In the above example, V1, V2, V3, etc are the vertices.
- Edge: An edge in the figure above is represented by the lines connecting two vertices. An edge can be uni-directinal or bi-directional. The direction is usually represented by the arrow. Bi-directional edges usually do not have arrow heads. In the above examples, E1, E2, E3, etc are edges. Note that E1 and E6 are bi-directional while the rest are uni-directional.
How to Represent a Graph in a Code?
In the previous section we show some examples how real-world data like train stations or even a computer code can be represented as a graph. In this section we would like to discuss how such graphs are written in a computer code. The main information needed by the computer is the following:
- what are the vertices
- what are the edges
- how the vertices are connected by the edges
Adjacency Matrix
One way to represent this is to use an Adjencency Matrix. In this matrix, if there is a connection between one vertex to another, the cell between that row and column is represented by some number, e.g. 1 instead of 0 as when there is no connection. For example, the last graph above can be written in the following matrix:
| V1 | V2 | V3 | V4 | V5 | |
|---|---|---|---|---|---|
| V1 | 1 | 1 | |||
| V2 | 1 | 1 | 1 | ||
| V3 | 1 | ||||
| V4 | 1 | 1 | |||
| V5 | 1 |
Note the following:
- The connection from vertex u to vertex v is represented by a non-zero value at row u and column v.
- For example, there is an edge from V1 to V2, so there is a 1 entry at row V1 and column V2. Similarly, there is an edge from V4 to V3 and this is represented by a 1 at row V4 and column V3.
- If the edge is bi-directional, we have a symmetry in the entry. For example, V1 is connected to V2 with a bi-directional edge. We see a non-zero entry at row V1 and column V2 as well as row V2 and column V1. Similarly between V2 and V3.
The advantage of this representation is that it is simple and intuitive. The only thing is that it may end up in a sparse matrix where most of the entry are zeros and only a few non-zero entry. So this is good when the number of edges is large such as when every vertex is connected to every other vertices.
Adjacency List
Another way to represent a graph is to use adjacency list. This is more suitable when the number of edges is not large. We can use a dictionary for this purpose:
graph1 = {'V1': ['V2', 'V5'],
'V2': ['V1', 'V3', 'V4'],
'V3': ['V2'],
'V4': ['V1', 'V3'],
'V5': ['V4']}
Notice that the keys are all the vertices in the graph and the value of the dictionary is a list of all the adjacent vertices connected to that particular vertex. For example, vertex V1 is connected to two other vertices V2 and V5. In fact, since there is no particular sequence for the adjacent vertices, you need not use a list and can use a dictionary instead as in the following:
graph1 = {'V1': {'V2': 1, 'V5': 1},
'V2': {'V1': 1, 'V3': 1, 'V4': 1},
'V3': {'V2': 1 },
'V4': {'V1': 1, 'V3': 1},
'V5': {'V4': 1}}
The value in the dictionary of the adjacent vertices are all 1 for this example, but they need not be. These values are called the weights or the costs. You can assign different weights. For example, in the graph for the MRT train, you can assign more cost to connection between Tampines Downtown Line to Pasir Ris or Simei East West Line if passanger has to go out from the MRT station from one line to the other line.
Using Object Oriented Programming
You have learnt Object Oriented programming in the previous week. We can apply this programming concept to represent a graph. We can create two classes:
VertexclassGraphclass
The Vertex class is similar to each entry in the dictionary. This class contains information on that particular vertex and who are the neighbouring or adjacent vertices connected this particular vertex. This class can also contains the weights of the connection between this vertex to its neighbours. The Graph class, on the other hand, contains the list of all the vertices in the graph. Each of this vertex is of the type Vertex. We can draw the UML diagram of these two classes as follows.
The above UML diagram shows that a `Graph` is composed of one or more `Vertex` objects. This is another _composition_ relationship between two classes.
We can specify the attributes and methods for both classes as shown in the image below.
The class `Graph` has an attribute called `vertices`. This attribute contains all the vertices in the graph where each vertex is of the type `Vertex`. This class has several methods like how to create or retrieve a `Vertex` object in the graph, add an edge between two vertices given their starting and ending `id`s. It may also have some other helper methods like to get all the neighbouring vertices of a given `Vertex` or to get the number of vertices in the graph. You can design some other methods but these are some of the common operations we may want to perform with a graph.
The class Vertex has two attributes. The first one is the id or the label for the Vertex object and the second one is its neighbouring Vertex objects. The class has some basic operation such as to add a neighbouring Vertex to the current Vertex object, or to get all the neighbouring Vertex objects of the current Vertex. Lastly, it also has a method to get the weight of the edge to the neighbouring Vertex object. Similarly, you can think of some other operations of a Vertex object that may not be listed above.