By the end of this lesson, you should be able to:
- Write functions to do binary heap data structure operation
- Implement heapsort using iteration
Important words:
- tree
- binary tree
- root
- heap
- heap property
- heapify
- node
- leaf
- parent node
- child node
- heapsort
Introduction
Previously, we discussed two sorting algorithms called Bubble Sort and Insertion Sort. In this section we will apply our programming skills to investigate another sorting algorithm called the Heapsort. We will then compare the performance of Heapsort with the previous Bubble Sort and Insertion Sort. We will discuss some notations on how to analyze these performance.
One reason why we introduce different sorting algorithms is to show you that there are many ways to solve the same problems. At the same time, these different ways may have different performances. After we introduce binary heap and heapsort algorithm, we will begin to introduce you how to analyze these different algorithms in terms of computation time. You will notice that Heapsort algorithm is a much better sorting algorithm as compared to Bubble sort and Insertion sort algorithms.
Binary Heap
Before, discussing Heapsort algorithm, we have to introduce a new data structure called binary heap or simply called heap. The heap is an array of object that we can view as a nearly perfect binary tree (or we can call it a complete binary tree).
A perfect binary tree is a full binary tree which all leaf nodes are at the same level. Complete binary trees are nearly perfect except the last level and all the leaves at the last level are packed towards the left.
You are familiar with the concept of array. But what is a binary tree? The easiest way to explain it is using some examples. The image below shows you an array of integers.
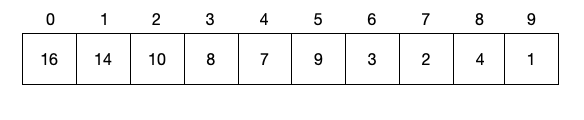
We have indicated the indices of each element in the array, which starts from 0. We can visualize the elements in this array in a form of a tree as shown below.
A tree in computer science is up-side down. It consists of nodes and it has one root node, which is at the top. In a binary tree, each node has only two children, which we will call the left child and the right child. Every node, except the root, has a parent node. The node without children is what we called a leaf.
Let’s take a look at the example above and put in all the terms we have mentioned:
- In the above tree, we have 10 nodes, where each node is each element in the array.
- The root node is the element 16, which has an index 0 in the array.
- Node with element 16 (root node) has two children. The left child is a node with the element 14, while the right child is a node with the element 10.
- Elements 9, 3, 2, 4, and 1 are all leaves because they do not have any children.
- The node with element 7 (index 4) has only one child, which is the node with element 1 (index 9).
- The node with element 1 (index 9) has node with index 4 as its parent.
Now, let’s go back to our definition of a heap. The heap is an array of object that we can view as a nearly perfect binary tree.
- A binary tree is a tree where all the nodes have only a maximum of two children, which you can call left child and right child.
- A full binary tree is a tree where all the nodes except the leaves have two children. In our case, heap is a complete binary tree and not a full binary tree. A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible. A complete binary tree is similar to a full binary tree with two major differences: all the leaf elements must lean toward the left and the last leaf element may not have the right sibling.
- The root of the tree is the node with index 0.
- We put the elements of our array into our tree from top to bottom and left to right sequence. With this, we can calculate the index of the children and the parent for every node.
Indices of Children and Parent in a Heap
Let’s start by considering how to calculate the index of the parent node. Let’s take a look at the example tree we have considered.

Note the following:
- The parent of node index 1 is 0. Similarly, the parent of node index 2 is also 0.
- The parent of node index 3 and 4 is 1, while the parent of node index 5 and 6 is 2.
How do we get index 0 from both indices 1 and 2? And how do we get index 1 from indices 3 and 4? Or index 2 from indices 5 and 6?
def parent(index):
Input: index of current node
Output: index of the parent node
Steps:
1. return integer((index-1) / 2)
We can test the above pseudocode. $(1-1)/2 = 0$ and $(2-1)/2 = 0$ for the second level nodes. Similarly, $(3-1)/2 = 1$ and $(4-1)/2 = 1$ for the third level nodes with the parent index 1. And $(5-1)/2 =2$ together with $(6-1)/2= 2$ for the third level nodes with the parent index 2. Note that we use integer division to get the correct parent node.
In order to get the index of the left child, let’s observe the following:
- The left child of node 0 is index 1.
- The left child of node 1 is index 3.
- The left child of node 2 is index 5.
- and so on.
We can get the left child index using the following:
def left(index):
Input: index of current node
Output: index of the left child node
Steps:
1. return (index * 2) + 1
Test the above pseudocode and ensure it gives the correct left child nodes.
Similarly, we can observe the following for the indices of the right child nodes:
- The right child of node 0 is index 2.
- The right child of node 1 is index 4.
- The right child of node 2 is index 6.
- and so on.
We can get the right child index using the following:
def right(index):
Input: index of current node
Output: index of the right child node
Steps:
1. return (index + 1) * 2
You can verify the above code yourself.
Heap Property
There are two kinds of heap: max-heaps and min-heaps. In this case we will discuss only max-heaps. Both heaps must satisfy the heap property, which specifies the kind of heap we are dealing with. The max-heap property is specified as follows:
For all nodes except the root:
A[parent(i)] >= A[i]
This means that in a max-heap, the parent nodes are always greater that their children. This also implies that the largest node is at the root. The figure below is an example of a max-heap because it satisfies the condition above.

Heapify - Maintaining the Heap Property
We will now describe an algorithm on how to maintain the heap property and in this example is the max-heap property. We will call this procedures to maintain the max-heap property as max-heapify. The idea is that for a given node, we will push down this node in such a way that the max-heap property is satisfied. This assumes that the left child of the given node forms a tree that satisfies max-heap property. Similarly, the right child of the given node forms a tree that satisfies max-heap property. The only part that does not satisfy the max-heap property is the current node and its two children.
(P)roblem Statement
Given an index of a node in a binary tree, where the left and the right children of that node satisfies the max-heap property, restore the max-heap property of the tree starting from the current node.
Input: index of the current node in a heap
Output: None
Process: re-order the elements in the heap
in such a way that the max-heap property is satisfied
from the current index node.
assumption:
- left child forms a tree that satisfies max-heap property
- right child forms a tree that satisfies max-heap property
- current node with its children may not satisfy max-heap property
Test (C)ase
Let’s take a look at the tree below.
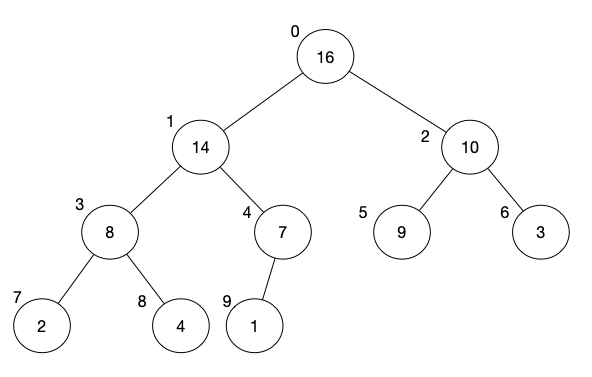
Note the following:
- The current node is index 1, which has the element of 4.
- The current with its children does not satisfy the max-heap property because $4 < 14$ and $4 < 7$.
- The left child, i.e. tree starting from index 3 (elements 14, with children of 2 and 8), forms a tree that satisfies the max-heap property.
- The right child, i.e. tree starting from index 4 (element 7, with one children of 1), forms a tree that satisfies the max-heap property.
The procedure of max-heapify will push the current node by swapping with the largest node along the way to satisfy the max-heap property. To do that, in the process of pushing the nodes, we will swap that node with the largest child. In this way, we satisfy the max-heap property.
Let’s look at the particular example above. Given the tree above, we do the folloing:
-
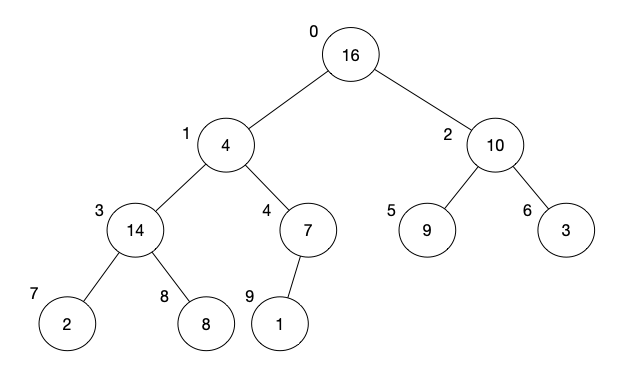
We first find the largest child of the current node. The current node is element 4 (index 1). The largest child is element 14 (index 3), which is the left child of the current node.

-
We then swap the current node with the largest child, i.e. element 4 (index 1) with element 14 (index 3).
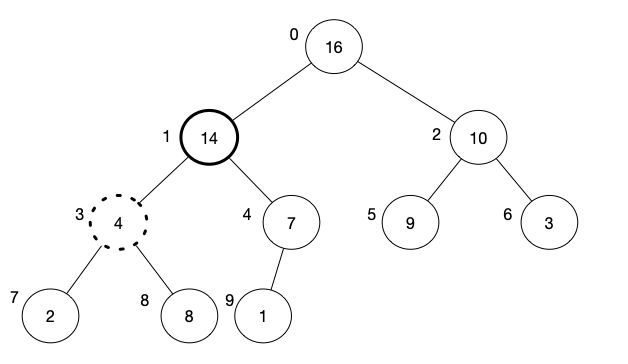
- We, then, move our current index to the place where we swap, i.e. old index of element 14. So we are now at index 3.
-
We do the same thing by looking if any of the children is larger than the current node. Since $8 > 4$, we swap 4 (index 3) with 8 (index 8).
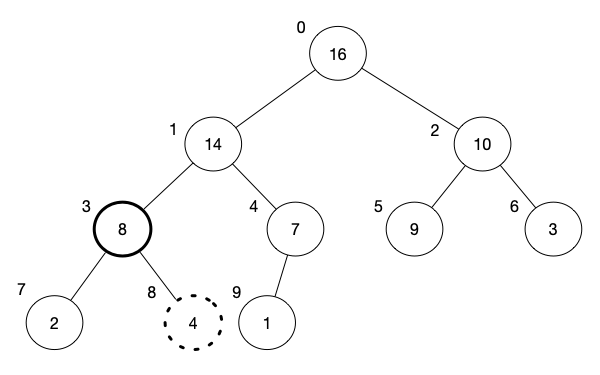
- We, then, move our current index to the place where we swap, i.e. old index of element 8. So we are now at index 8.
- Since this node has no more children, we stop. We can check whether the node has more children by calculating the index of the left child and see if it is still within the length of the array minus one, i.e. $left(i) < n-1$, where $i$ is the current node index and $n$ is the number of element in the array.
(D)esign of Algorithm
We can write down the steps we did in the previous section as follows.
def max-heapify(A, i):
version: 1
Input:
- A = array storing the heap
- i = index of the current node to restore max-heap property
Output: None, restore the element in place
Steps:
1. current_i = i # current index starting from input i
2. As long as ( left(current_i) < length of array), do:
2.1 max_child_i = get the index of largest child of the node current_i
2.2 if array[max_child_i] > array[current_i], do:
2.2.1 swap( array[max_child_i], array[current_i])
2.3 current_i = max_child_i # move to the index of the largest child
Note that the above steps will continue iterating down even if the current node already satisfies max-heap property. This means that we can stop iterating if the largest children is already less than the current node. We can do this by checking if any swap is happening. If no swap is needed then we are done. This is because we assumes that the left child and the right child already satisfies max-heap property.
def max-heapify(A, i):
version: 2
Input:
- A = array storing the heap
- i = index of the current node to restore max-heap property
Output: None, restore the element in place
Steps:
1. current_i = i # current index starting from input i
2. swapped = True
3. As long as ( left(current_i) < length of array) AND swapped, do:
3.1 swapped = False
3.2 max_child_i = get the index of largest child of the node current_i
3.3 if array[max_child_i] > array[current_i], do:
3.3.1 swap( array[max_child_i], array[current_i])
3.3.2 swapped = True
3.3 current_i = max_child_i # move to the index of the largest child
Note:
- We introduced a boolean variable called
swapped. At every iteration, we setswappedtoFalse. - If there is a swap, we set this boolean variable to
Trueand continues to the next iteration. - If there is no swap, the boolean variable is still
Falseand so it will stop the iteration.
Building a Heap
We can then use the previous procedure max-heapify to build a binary heap data structure from any arbitrary array. The idea is to go through every nodes in the tree and heapify them. However, we need not do for all the nodes, but rather only half of those nodes. The reason is that we do not need to heapify the leaves.
We can show that the elements in the array from index $n/2$ to $n-1$ are all leaves. We do not need to push down these nodes as they do not have any children. So we can stry from element at position $n/2 - 1$ and move up to element at position 0.
(P)roblem Statement
Given an arbitrary array, re-order the elements in such a way that it satisfies max-heap property.
Input: any arbitrary array of integers
Output: None
Process: Re-order the elements such that the whole array satisfies max-heap property
Test (C)ases
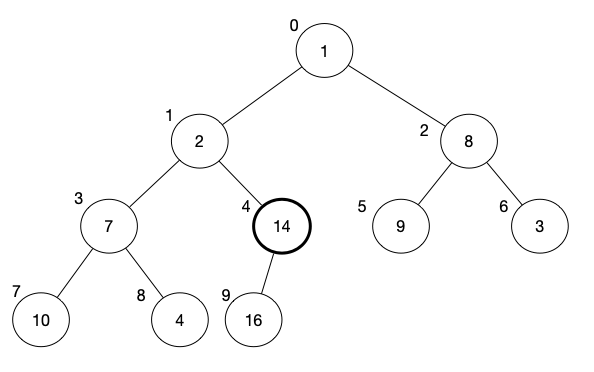
Let’s consider an array as shown below.
[1, 2, 8, 7, 14, 9, 3, 10, 4, 16]
-
We first visualize this array as a binary tree as shown below. Note that this tree does not satisfy max-heap property.
-
We will start from the middle index, i.e. $n/2 - 1 = 10/2 - 1 = 4$, which is the fifth element, i.e. 14. Notice that all the elements after 14 are all leaves. We call max-heapify on 14 and the result is a swap between 14 and 16. We only have one iteration because now 14 has reached the end of the array and cannot be compared with any other nodes. In the figure below, we indicate the next element to consider with a dotted circle.
[1, 2, 8, 7, 14, 9, 3, 10, 4, 16]
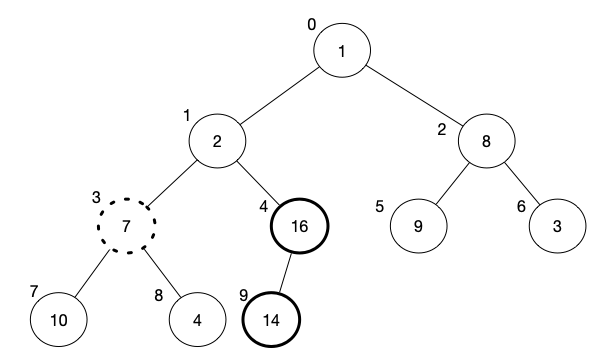
[1, 2, 8, 7, 16, 9, 3, 10, 4, 14]
-
Now we move to the element on the left of 16, which is 7. The result of max-heapify will swap 7 with 10.
[1, 2, 8, 7, 16, 9, 3, 10, 4, 14]
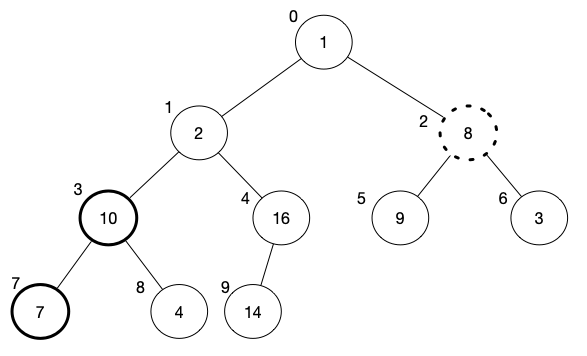
[1, 2, 8, 10, 16, 9, 3, 7, 4, 14]
-
Now, we move to the next element, which is 8. The result of max-heapify will swap 8 with 9.
[1, 2, 8, 10, 16, 9, 3, 7, 4, 14]
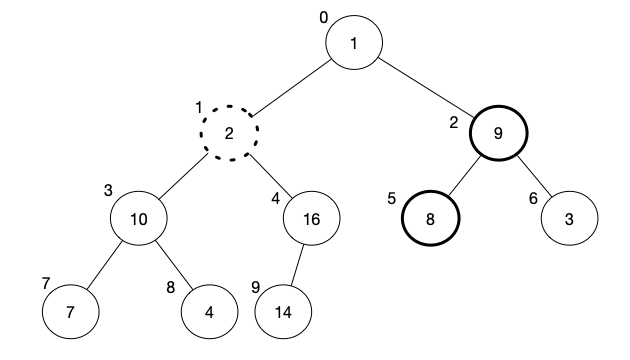
[1, 2, 9, 10, 16, 8, 3, 7, 4, 14]
-
We move on to the next element, which is 2. The result of max-heapify will swap 2 with 16, and then 2 with 14.
[1, 2, 9, 10, 16, 8, 3, 7, 4, 14]
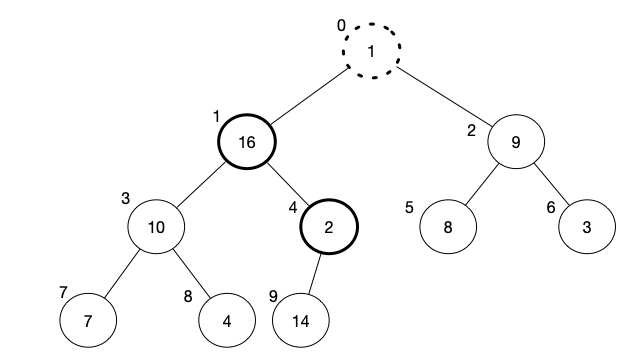
[1, 16, 9, 10, 2, 8, 3, 7, 4, 14]
and then,
[1, 16, 9, 10, 2, 8, 3, 7, 4, 14]
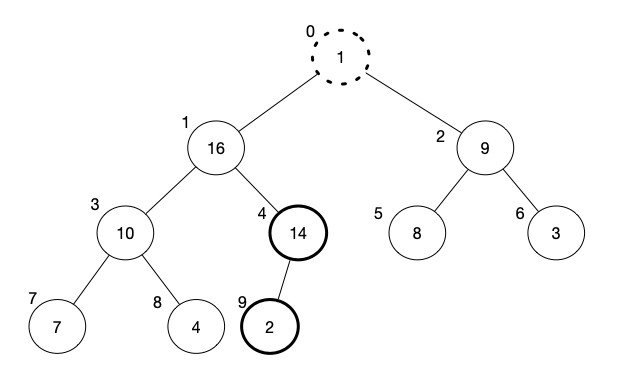
[1, 16, 9, 10, 14, 8, 3, 7, 4, 2]
-
And now we move to the last element, which is 1. The result of max-heapify will swap 1 with 16, and then 1 with 14, and finally 1 with 2.
[1, 16, 9, 10, 14, 8, 3, 7, 4, 2]
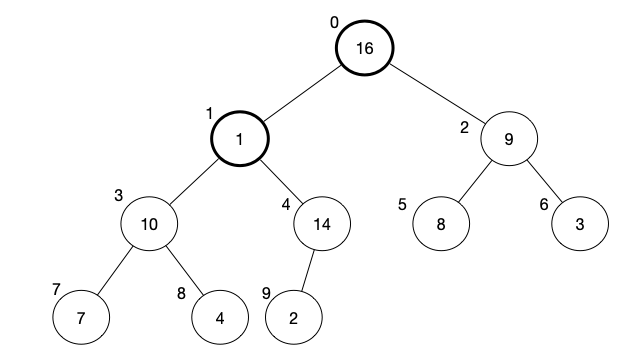
[16, 1, 9, 10, 14, 8, 3, 7, 4, 2]
next,
[16, 1, 9, 10, 14, 8, 3, 7, 4, 2]
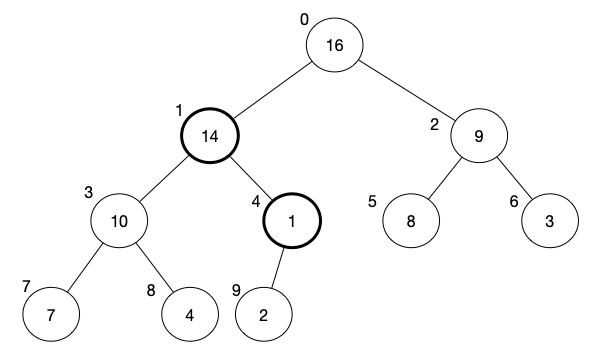
[16, 14, 9, 10, 1, 8, 3, 7, 4, 2]
lastly,
[16, 14, 9, 10, 1, 8, 3, 7, 4, 2]
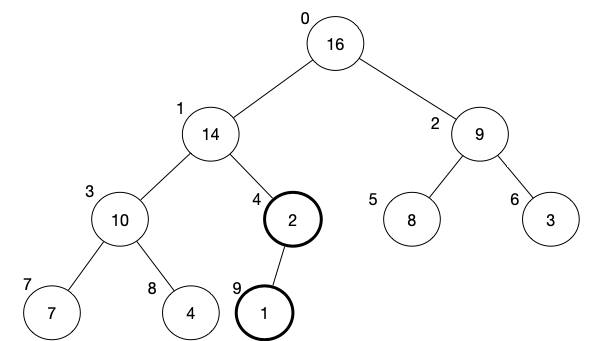
[16, 14, 9, 10, 2, 8, 3, 7, 4, 1]
-
Once it reaches the last element, the whole array now satisfies the max-heap property.
(D)esign of Algorithm
We can then write down the steps in a pseudocode as follows:
def build-max-heap(array):
Input:
- array: arbitrary array of integers
Output: None, sort the element in place
Steps:
1. n = length of array
2. starting_index = integer(n / 2) - 1 # start from the middle or non-leaf node
3. For current_index in Range(from starting_index down to 0), do:
3.1 call max-heapify(array, current_index)
Note:
- The pseudo simply says, we start from the middle node as our
starting_index, and call the function max-heapify on that node. - We then move to the left and continues calling max-heapify until we reach the first element at index 0.
Heapsort
Now, we can consider Heapsort algorithm. The idea of a heapsort is pretty simple. For any arbitrary array, we can sort the integers in the array by first building a max-heap. Once the max-heap is built, we know that the maximum is at the root node. With this, we can swap the root node with the last element and then exclude it from our heap. We then should restore the max-heap property after this swap because now the root node will be a small number. We can do this repetitively until there is no more element in the heap.
(P)roblem Statement
Given an arbitrary array of integers, sort the element using heapsort algorithm.
Input: array of integers
Output: None
Process: Sort the elements of the array in place using heapsort
Test (C)ases
Let’s use the same example as in the previous seciton. Let’s say we have the following array.
[1, 2, 8, 7, 14, 9, 3, 10, 4, 16]
We will sort the elements following these steps:
-
Build a max-heap from this array. The previous section has shown that the final output of building a max-heap will be:
[16, 14, 9, 10, 2, 8, 3, 7, 4, 1]
-
Now, we will swap the largest element with the last element, and exclude it from the heap. We will put the excluded element in what we called as sorted of the list. This sorted section is separated by
||in the list below.heap = [1, 14, 9, 10, 2, 8, 3, 7, 4 , 16] -
Notice, now, that the array does not satisfy the max-heap property. So we must max-heapify the array to push the element 1 down to its place. The process of max-heapify from the root node will result in:
heap = [1, 14, 9, 10, 2, 8, 3, 7, 4, 16] heap = [14, 1, 9, 10, 2, 8, 3, 7, 4, 16] heap = [14, 10, 9, 1, 2, 8, 3, 7, 4, 16] heap = [14, 10, 9, 7, 2, 8, 3, 1, 4, 16] -
Once we have restored the max-heap property, we can take out the largest element from the first element and swap it with the last element in the heap.
heap = [4, 10, 9, 7, 2, 8, 3, 1, 14, 16] -
We then max-heapify the heap again to restore the max-heap property.
heap = [4, 10, 9, 7, 2, 8, 3, 1, 14, 16] heap = [10, 4, 9, 7, 2, 8, 3, 1, 14, 16] heap = [10, 7, 9, 4, 2, 8, 3, 1, 14, 16] -
We then swap the largest element with the last element in the heap, and take it out from the heap.
heap = [1, 7, 9, 4, 2, 8, 3, 10, 14, 16] -
The same process of max-heapify happens again. We will now remove the intermediate step and only show the first and the final state of the heaps.
heap = [1, 7, 9, 4, 2, 8, 3, 10, 14, 16] heap = [9, 7, 8, 4, 2, 1, 3, 10, 14, 16] -
We swap and take out again the largest element. The next iteration would be:
heap = [3, 7, 8, 4, 2, 1, 9, 10, 14, 16] then we max-heapify the array:
heap = [8, 7, 3, 4, 2, 1, 9, 10, 14, 16] Swapping and taking out the largest element:
heap = [1, 7, 3, 4, 2, 8, 9, 10, 14, 16] and max-heapify:
heap = [7, 4, 3, 1, 2, 8, 9, 10, 14, 16] Swapping and taking out the largest element:
heap = [2, 4, 3, 1, 7, 8, 9, 10, 14, 16] and max-heapify:
heap = [4, 2, 3, 1, 7, 8, 9, 10, 14, 16] Swapping and taking out the largest element:
heap = [1, 2, 3, 4, 7, 8, 9, 10, 14, 16] and max-heapify:
heap = [3, 2, 1, 4, 7, 8, 9, 10, 14, 16] Swapping and taking out the largest element:
heap = [1, 2, 3, 4, 7, 8, 9, 10, 14, 16] and max-heapify:
heap = [2, 1, 3, 4, 7, 8, 9, 10, 14, 16] Swapping and taking out the largest element:
heap = [1, 2, 3, 4, 7, 8, 9, 10, 14, 16] -
At this point in time, the array is already sorted. If
heapandsortedare not a separate array but rather one single array, we will have:result = [1, 2, 3, 4, 7, 8, 9, 10, 14, 16]
(D)esign of Algorithm
Let’s write down the steps in the previous section in a pseudocode.
def heapsort(array):
Input:
- array: any arbitrary array
Output: None
Steps:
1. call build-max-heap(array)
2. heap_end_pos = length of array - 1 # index of the last element in the heap
3. As long as (heap_end_pos > 0), do:
3.1 swap( array[0], array[heap_end_pos])
3.2 heap_end_pos = heap_end_pos -1 # reduce heap size
3.3 call max-heapify(array[from index 0 to heap_end_pos inclusive], 0)
Note:
- We first call the procedure in the previous section called
build-max-heapto create the max-heap data structure. - We then start from the last element in the heap and swap it with the largest element (always at index 0).
- We reduce the variable
heap_end_posto reduce the heap size and exclude the largest element from the heap. - Then, we can call
max-heapifyon a subarray. The subarray starts from index 0 of the current array up to indexheap_end_pos. In this way, we exclude the largest element from being max-heapified. - The second argument of
max-heapifyis the starting node where the process should begins. In this case, we always want to startmax-heapifyfrom index 0 because this is the node where we replace the largest element with some small element from the end of the heap.