By the end of this lesson, you should be able to:
- Apply breadth first search to perform state-space search
Important words:
- state space search
- legal inputs
- state map
- graph traversal
- breadth first search
- queue
- path
- step
Introduction
Previously we have learnt on how we can find data from a graph data structure. We implemented breadth-first search and explore depth-first search algorithm. We can look into this problem from a different angle as a state-space search. Instead of thinking about nodes and edges, we can see it as states and transitions. Each node can be thought of as one state and each edge can be thought of as a transition from one state to anther state. We can then apply graph algorithm for our state machines.
But what does it mean of doing a state-space search? Remember that we attach every transition from one state to another state with an input that moves that state machine from the current state to the next state. Doing a state-space search allows us to find a path or sequence of inputs that bring us from a starting state to a goal state. This means that if I know my goal state of my machine, I can do a search what are the inputs needed to reach that state. This can be used to make our state machine more intelligent through planning.
Defining State-Space Search
Let’s first define our problem. We can model this state-space search problem as follows. Given the following information:
- a set of states the system can be in;
- a starting state;
- a goal test, which is a procedure that can be applied to any state, and returns the True if that state is the goal state;
- a successor function, which takes a state and an action as input, and returns the new state that results from taking the action in that state;
- and a legal action list, which is just a list of actions that can be executed in this domain the problem is to find a sequence of input that brings us to the goal state given the starting state.
Let’s take a look an an example. Consider the case where we have the following states:
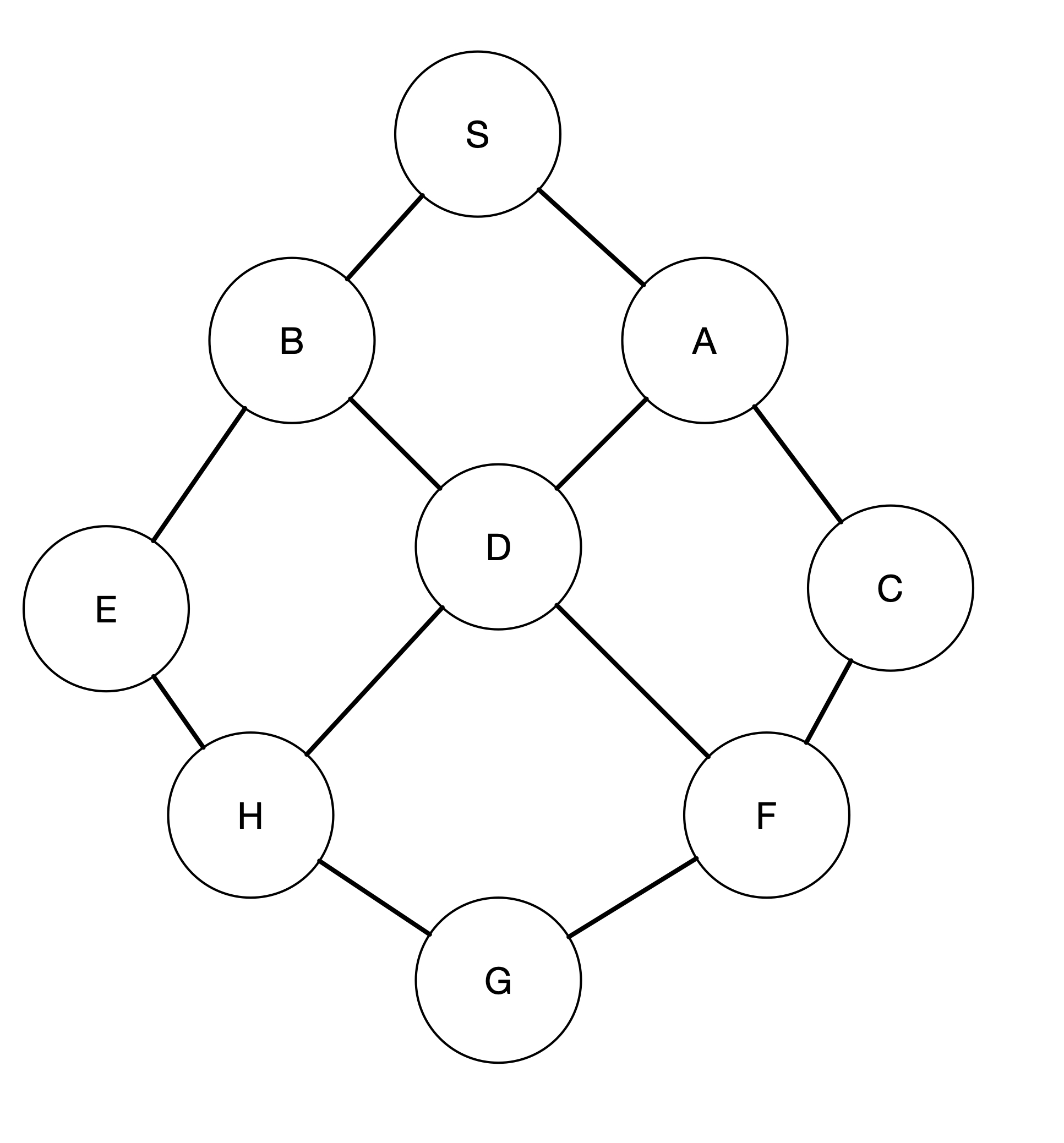
We do not draw any arrow in the above diagram to simplify the drawing as we assume that the transition is bi-directional. This means that there is a transition from S to A and from A to S.
In the above example, we have the set of states:
\[states = \{`S`, `A`, `B`, `C`, `D`, `E`, `F`, `G`, `H`\}\]We also need to know the starting state, so let’s say state ‘S’ is the starting state. The goal test is a function that takes in a state as an input and returns True if that state is the goal state. So if we want to reach G starting from S, we can write the following goal test.
def goal_test(state):
return state == 'G'
We can also write it as a lambda function in Python as follows.
lambda state: state == 'G'
The legal actions in this domain can be integers values like $0, 1, \ldots, n-1$, where $n$ is the maximum number of successors in any of the states. The maximum number of successors simply means the maximum number of degrees in the graph. We can find this number by looking at the node (or state) that has the largest number of edges. In this case, state ‘D’ has the largest number of edges, i.e. 4. So the legal actions are integer values: 0, 1, 2, 3. We can assign, for example, the following transitions:
- input 0: transition from D to A
- input 1: transition from D to B
- input 2: transition from D to F
- input 3: transition from D to H
Therefore, we also need a kind of transition maps. If our legal input is integer values, we can simply use a list where the index matches the transition. We can write our transition map as follows.
statemap = {'S': ['A', 'B'],
'A': ['S', 'C', 'D'],
'B': ['S', 'D', 'E'],
'C': ['A', 'F'],
'D': ['A', 'B', 'F', 'H'],
'E': ['B', 'H'],
'F': ['C', 'D', 'G'],
'G': ['F', 'H'],
'H': ['D', 'E', 'G']}
Notice in the above dictionary that we use list in the same sequence for state D, i.e.
'D': ['A', 'B', 'F', 'H'],
This allows us to have transition as specified above. For example,
statemap['D'][0] # returns state A
statemap['D'][1] # returns state B
statemap['D'][2] # returns state F
statemap['D'][3] # returns state H
Given the above dictionary, we can simply write our successor function as follows.
def statemap_successor(state, action):
return statemap[state][action]
We may need some additional test to ensure that if an action that does not exist from that current state, it will just remain in the current state. For example, state ‘G’ has two transitions, we should expect the following.
print(statemap_successor('G', 2)) # output 'G'
The above code should output ‘G’ because there is only two transition and so action 2 which index the third transition does not exist.
Search Trees
Our state-space search can be represented as a search tree having the starting state as its root. For example, if we want to search path from state S to state D, we can draw the following search tree.
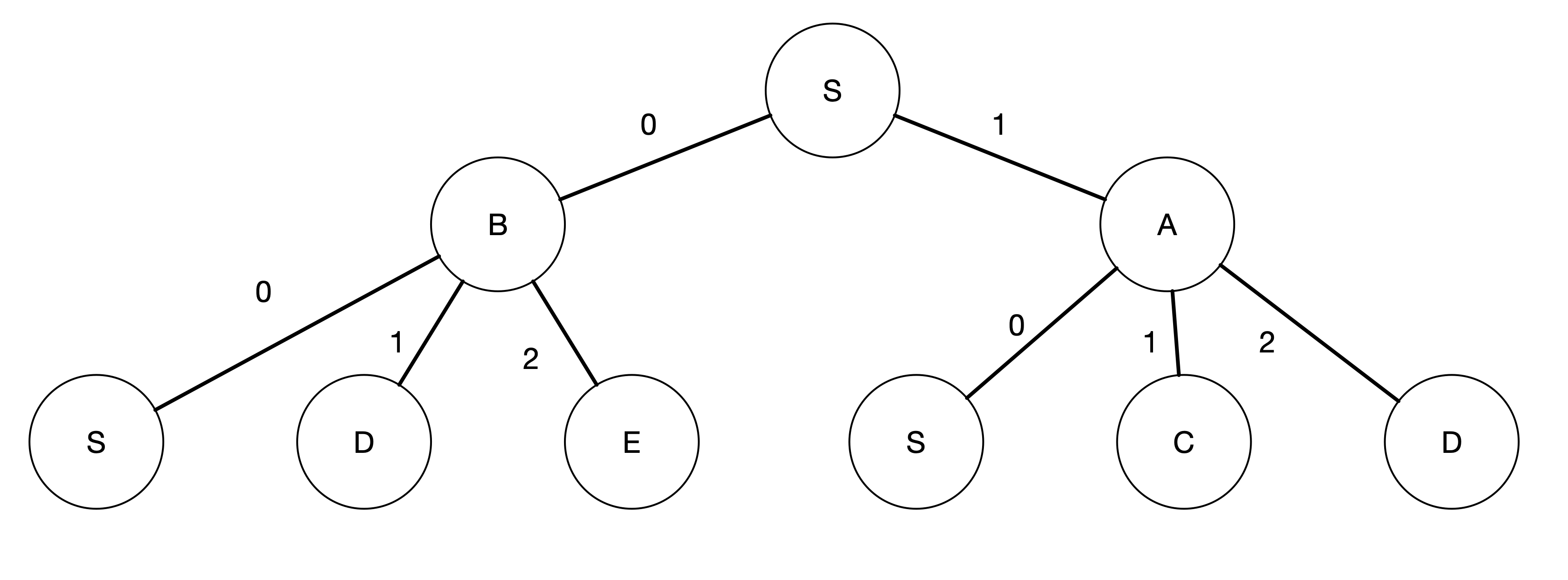
In the above tree, we label the edges with the input action that one takes from one state to another state following the statemap dictionary in the previous section. If we can build this tree, we can find the path from S to D and we know that we need to take the following actions:
- Take 0 from S to reach B
- Take 1 from B to reach D or we can also take the following sequence of actions:
- Take 1 from S to reach A
- Take 2 from A to reach D
Class SearchNode
We can facilitate this search by creating a class called SearchNode that contains the information needed to build the search Trees. The UML diagram for SearchNode is shown below.
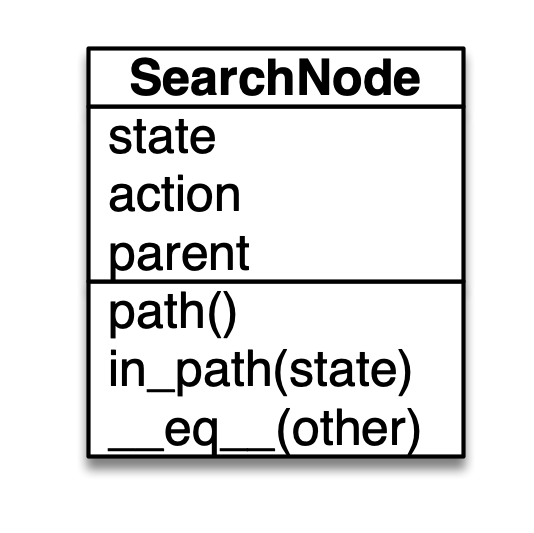
The class has three attributes:
- state, which identifies the node for the particular state it represents in the tree
- action, which stores the action it takes from the parent to reach the current node
- parent, which stores the reference to the parent node in the search tree
The class has three methods:
path()which returns the path from the root of the tree to the current nodein_path(state)which takes in a state and check if that state is in the path from the root to the current node__eq__(other)which allows us to use the equality operator in Python to check if two nodes are equal
You will work on the implementation of this class in your Problem Set.
State Machine for State-Space Search
We have been looking into this search problem from the perspective of state machine. This implies that we can create a state machine class to represent a state machine that does state-space search. This class, however, has unique requirements as you need to make sure you have enough information for the problem. This means that you may want to ensure that such class must provide information about the following:
statemap, which gives you the transition relationship from one state to another with respect to the legal inputlegal_inputs, which is a set of legal inputs in this domain.
We can enforce this in Python using the Abstract Base Class and creating an abstract property. This is a similar concept as how we implement the computed property start_state. We can, thus, define the following class:
from abc import abstractmethod
class StateSpaceSearch(StateMachine):
@property
@abstractmethod
def statemap(self):
pass
@property
@abstractmethod
def legal_inputs(self):
pass
@property
@abstractmethod
def start_state(self):
return self.__start_state
@start_state.setter
@abstrctmethod
def start_state(self, value):
self.__start_state = value
In the above definition, StateSpaceSearch class inherits from StateMachine class and it adds the required property statemap and legal_inputs. Any state machine class implementing StateSpaceSearch now must define these two properties and its getter method. The last two abstract methods that we have is simply the getter and the setter of start_state computed property which has to be implemented for all StateMachine child class. We created a general implementation that sets and returns the attribute __start_state. We use Python name mangling with double underscore at the beginning of the variable to keep this attribute hidden.
So now, what we need to do is simply to implement the two abstract methods, i.e. statemap and legal_inputs, as well as initializing the start_state property. For example, we can initialize the start_state property and implement the statemap property as follows:
class MapSM(StateSpaceSearch):
def __init__(self, start):
self.start_state = start
@property
def statemap(self):
statemap = {"S": ["A", "B"],
"A": ["S", "C", "D"],
"B": ["S", "D", "E"],
"C": ["A", "F"],
"D": ["A", "B", "F", "H"],
"E": ["B", "H"],
"F": ["C", "D", "G"],
"H": ["D", "E", "G"],
"G": ["F", "H"]}
return statemap
Notice that the statemap must be defined in the child class that implements StateSpaceSearch because such mapping transition information can be different from one state machine to another. This cannot be defined in the base class.
Similarly, the computed property legal_inputs can take in the information from statemap and return a set of the legal inputs. Though we may think that the code to create such a set is the same for all state-space search, it actually depends on how one implements the statemap property. If one uses a list as in our case, such set will be a set of integer values. But if one uses a dictionary, the set legal_inputs may be a set of other data types used in the key of that dictionary.
In this state machine the start_state is the starting state of our search problem. For example, state ‘S’ should be initialized as our start_state following the previous examples.
We also need to define our get_next_values(state, inp) method. This method should return the next state and the output of our search transition. In our state-space search, the output is usually the same as the next state, which is what state should the machine go to given the current state and the input action. In fact, this function is exactly what a successor function statemap_successor(state, action) does in our previous discussion. This means that you can implement your get_next_values(state, inp) method using the information you have from statemap and legal_inputs. Remember to ensure that if the input is not valid for that current state, it should remain in the current state. And now you have a complete state machine to do state-space search.
You can write your breadth-first search algorithm and makes use of the get_next_values() of the state machine to find a path from the starting state to the goal state. You will do this in your Problem Set.