By the end of this lesson, you should be able to:
- Implement abstract data type for Stack, Queue using Object Oriented paradigm
- Apply Stack and Queue for some applications
- Implement Queue using double Stack and discuss implementation impact on computation time
Important words:
- data structure
- stack
- queue
- pop
- push
- enqueue
- dequeue
Introduction
You have encountered list as one of the built-in data types that Python support. You can use list to represent one dimensional or linear data collection where sequence and order matters. There are other kinds of linear data structures and we will explore some of them in this lesson.
Stack
Stack is a type of data structure that follows the LIFO (Last in First out) principle. Stack is common in daily life. Consider a stack of books.

Now, let’s think about what are the operations we can do with such a structure. We can do the following:
- We can add new book into the stack by putting it at the top. This operation is called a push.
- Or you can remove a book from the stack by taking the one at the top. This operation is called a pop.
- Or you can simply look at the book at the top of the stack. This operation is called a peek.
What you cannot do, however, are the following:
- insert a book somewhere in the middle of the stack
- take out a book from somewhere in the middle of the stack
If you want to do those two operations, you have to start by removing the books at the top first. This is why Stack is called Last in First out (LIFO). We can generalize this into an abstract concept of Stack data structure as shown below.

As you can see, there are three operations related to Stack:
- push
- pop
- and peek
We can create a stack using Object Oriented Programming by defining a class. A Stack class has at least the following attributes and methods.
Stack
Attributes:
1. items
Methods:
1. Push // insert
2. Pop // remove and read
3. Peek // only read
You can use this animation to get familiar with the Stack operation.
Queue
Queue is another common data structure that we find frequently in daily life. For example, the image below shows a queue of people to Louvre Museum.

Notice that Queue is different from Stack. Stack follows Last in First out principle. On the other hand, Queue follows the First in First out (FIFO) principle. The first person that enters the queue is the first person that can enter the Louvre Museum. We can abstract this as a kind of data structures shown below.

Queues are similar to Stacks in some manners. For example, you can’t access the elements in middle of the queue. This is like taking someone from the middle of the queue and let him or her enter the museum before those who are at the front of the queue. You can’t also insert an element to somewhere in the middle of the queue. This is called cutting queues. No one will be happy with this. So we can only access item from the front of the queue and insert an item from the rear of the queue. These are the two operations of Queues.
enqueueis to put an item from the rear of the queue,dequeueis to take an item out from the front of the queue,- and
peekis similar to Stack operation which is just to read the item at the front of the queue without removing it from the queue.
As such a Queue data structure must have at least the following attributes and methods:
Queue
Attributes:
1. items
Methods:
1. Enqueue
2. Dequeue
3. Peek
You can use this animation to get familiar with Queue operations.
Applications
How or when do we use such data structures like Stack and Queue. In this section we will illustrate two examples. The first one is an example of Stack’s application and the second one is an example for Queue’s application.
Post-Fix Expression Evaluation
One application that uses Stack data structure is to evaluate a Post-Fix Expression. Our mathematical expression is normally expressed as an infix notation. For example,
\[3 + 4 \times 2\]In this notation, $4 \times 2$ is evaluated first and the result is added to 3 to get the final result. In this notation, the operators are in between the operands. This is why it is called infix notation. But, this is not the only notation. We can represent the same mathematical operations using a Post-Fix notation. In this notation, the operators are placed before the operands justyifing its name, i.e. postfix. Let’s write the same mathematical expression using a post-fix notation.
\[4 2 \times 3 +\]In the above notation, we can see that the operators are placed after the operands. The first two numbers are the operands. The third one is an operator for multiplication. So we will multiply the first two numbers 4 and 2. The next one is another number, i.e. 3. And the last one is an addition operator. This means that we will add 3 with the result of the multiplication of 4 and 2.
How do we use Stack to evaluate post-fix notation? The steps are written below.
Post-Fix Evaluation Steps:
1. Read the expression from left to right.
2. If it is an operand (not an operator symbol), do the following:
2.1. put the operand into the stack.
3. Otherwise (this is an operator), do the following:
3.1. pop out the top of the stack as the *right* operand
3.1. pop out the top of the stack as the *left* operand
3.1. evaluate the operator with the operands
3.1. push the result into the stack
Program’s Stack
In fact, perhaps unknowingly, you have had an encounter with stacks just a week ago. Computer actually uses stacks in recursion! (Call stacks are an important concept in general programming too!) Let’s look at this in action with the factorial fuction. factorial(3), or 3! = 3*2*1. Here’s a recursive function to calculate the factorial of a number:
def factorial(x):
if x == 1:
return 1
else:
return x * factorial(x-1)
print(factorial(3))
You can visualize the Stack calls using Python Tutor. Notice that the computer treats the frames for factorial in a way like Stack operations that grows downward.
As mentioned, stacks are an important concept on how computer works. You may wonder why the name most voted for the most popular website for programmers is called Stack Overflow.
Radix Sort with Queue
We have seen how Stack is used to evaluate post-fix notation. Now, we will work with another algorithm called Radix sort to show how Queue can be used. Radix sort is a non-comparison sorting algorithm for integers by grouping integers by individual digits that share the same positon and value. It utilizes 10 “buckets” numbered from 0-9 to sort.
Radix sort will go through each digit of all numbers and put them in the buckets matching their digit, and take them out again, repeating until all digits are checked.
A simple animation for radix sorting:
Source: visualgo.net.
(Visualgo provides a lot of nice animations of many different algorithms that may help you visualize the algorithm better)
There are two kinds of Queues used in Radix sort:
- 1 x Main bin queue
- 10 x Radix bin queues
The Radix sort operation can be described as follows:
- First, put all the item into the Main bin queue.
- The next step is to start with the lowest digit. In this case, it is the ones digit. We take out all the items from the Main bin and put it into the respective radix bins. If the ones is 0, we put into radix bin 0. If the ones is 1, we put into the radix bin 1. If the ones is 2, we put into the radix bin 2, and so on until 9.
- Once we finish putting all the items into the respective radix bins, we empty out the radix bin queue and put the items back into the Main bin queue. We start from radix 0 and continue until radix bin 9.
- We repeat this step until we reach the highest digits.
Let’s give some example using four numbers: 101, 21, 4000, 7. We can rewrite these numbers up to four digits:
0101, 0021, 4000, and 0007.
We can then start from the lowest digit, the ones. As we take out the items from the Main bin queue, we do the following:
- put
010(1)into radix bin 1 - put
002(1)into radix bin 1 - put
400(0)into radix bin 0 - put
000(7)into radix bin 7
The radix bin will be filled as follows:
- Bin 0: 4000
- Bin 1: 0101, 0021
- Bin 2:
- Bin 3:
- Bin 4:
- Bin 5:
- Bin 6:
- Bin 7: 0007
- Bin 8:
- Bin 9:
Once we are done, we will take out the items from the radix bins and put it back into the Main bin queue. We do this starting from radix bin 0. The main queue now contains.
4000, 0101, 0021, 0007
Now, we are ready to do with the tens digit. We take out from the main bin queue to the radix bins.
- put
40(0)0into radix bin 0 - put
01(0)1into radix bin 0 - put
00(2)1into radix bin 2 - put
00(0)7into radix bin 0
The radix bin will be filled as follows:
- Bin 0: 4000, 0101, 0007
- Bin 1:
- Bin 2: 0021
- Bin 3:
- Bin 4:
- Bin 5:
- Bin 6:
- Bin 7:
- Bin 8:
- Bin 9:
Now, we will put back into the Main bin queue.
4000, 0101, 0007, 0021
We repeat again the steps for the hundreds.
- put
4(0)00into radix bin 0 - put
0(1)01into radix bin 1 - put
0(0)07into radix bin 0 - put
0(0)21into radix bin 0
The state of the radix bin will be as follows.
- Bin 0: 4000, 0007, 0021
- Bin 1: 0101
- Bin 2:
- Bin 3:
- Bin 4:
- Bin 5:
- Bin 6:
- Bin 7:
- Bin 8:
- Bin 9:
Lastly, we do the same steps for the thousands digit.
- we put
(4)000into radix bin 4 - we put
(0)007into radix bin 0 - we put
(0)021into radix bin 0 - we put
(0)101into radix bin 0
And the state of the radix bin will be as follows.
- Bin 0: 0007, 0021, 0101
- Bin 1:
- Bin 2:
- Bin 3:
- Bin 4: 4000
- Bin 5:
- Bin 6:
- Bin 7:
- Bin 8:
- Bin 9:
After we take out and put into the Main bin, we will have
0007, 0021, 0101, and 4000
or
7, 21, 101, 4000
which is the sorted arrangement of the numbers.
Queue with Double Stack
Queue data structure can be implemented in different ways. The first way that comes to our mind maybe simply to use a list as its internal storage. The problem with list is that one of the Queue operation will be slow. Why is this so? Consider if we use the following code to add item into the list:
def enqueue(self, item):
self.items.append(item)
In this example, whenever we add item into the Queue, we always add it to the back. This operation takes constant time $O(1)$. However, the removal part, must be written as
def dequeue(self):
return self.items.pop(0)
The problem with this implementation is that it is very slow. The reason is that Python has to move all the elements after index 0 one position to the left. This takes $O(n)$ where $n$ is the number of item in the Queue. This motivates us to think whether there is any other way of implementing Queue.
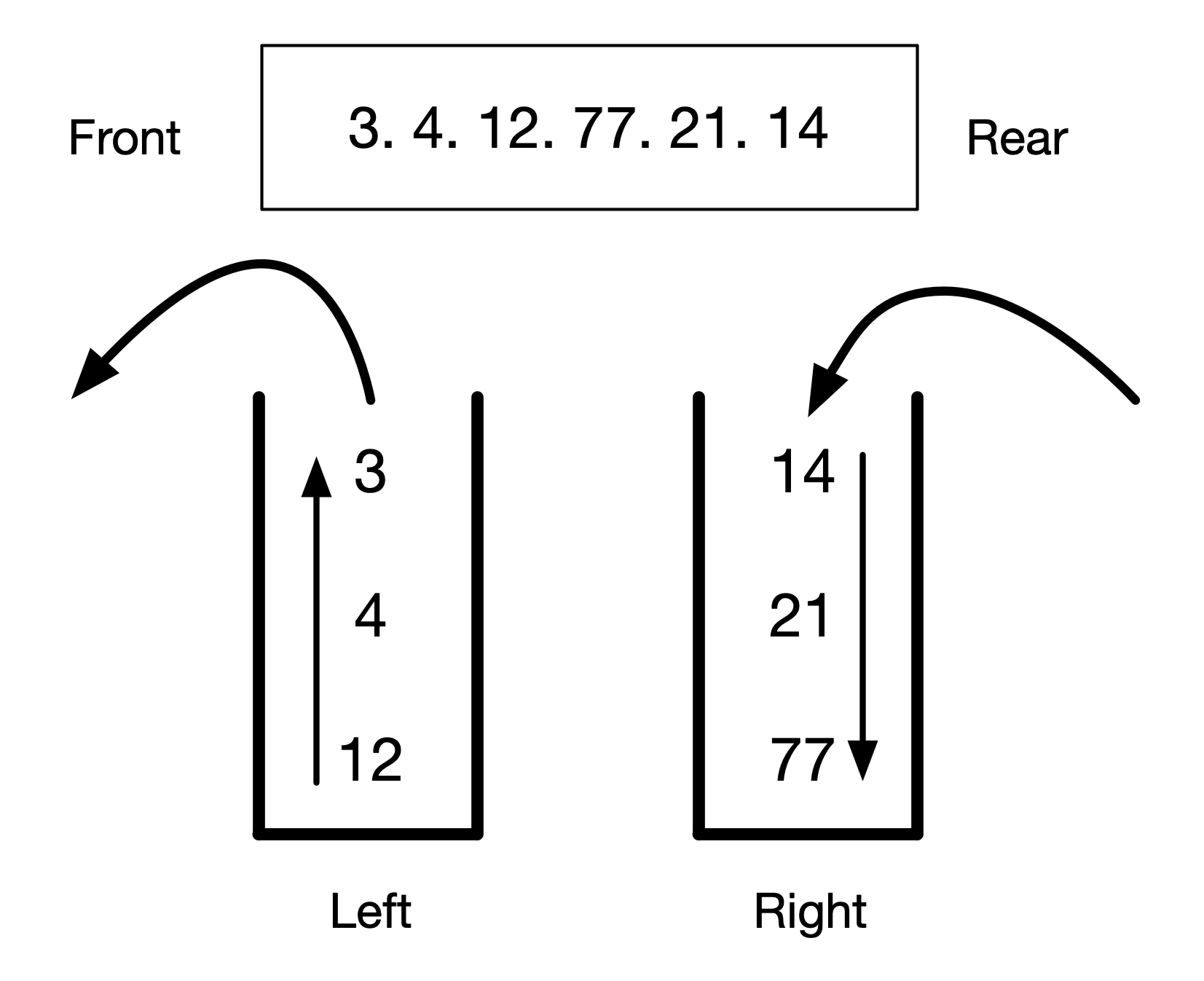
The answer is yes. We can use 2 Stack data structures as Queue’s internal storage. In this implementation, we have two stacks:
- Left Stack
- Right Stack
An example of a Queue implemented using 2 Stacks are shown below.
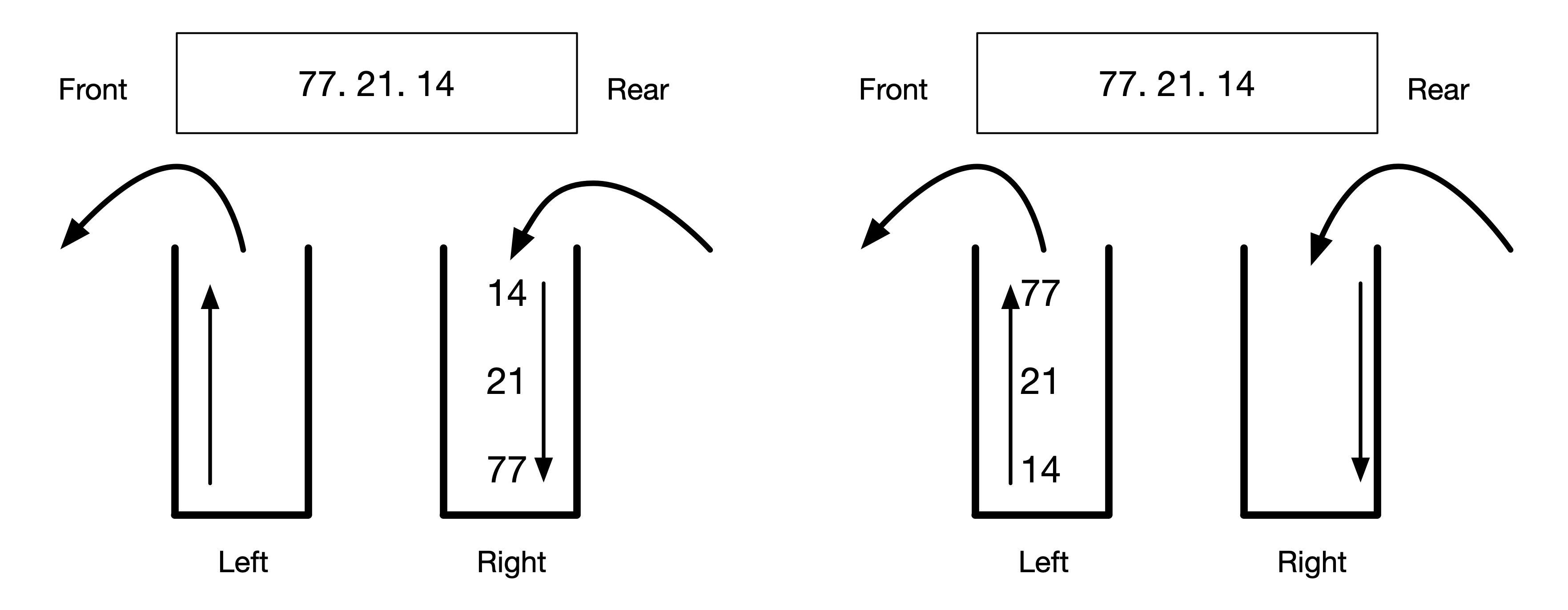
With this implementation both enqueue and dequeue are constant time $O(1)$. Recall that it takes constant time to add an item to the end of a list and to pop an item from the end of a list. What is tricky about this implementation is that when we try to dequeue an item while the Left Stack is empty. To do this we follow the following procedures:
- Copy all items from the Right Stack to the Left Stack.
- Reverse the items in the Left Stack.
- Remove the items on the Right Stack.
- Pop the requested item from the Left Stack.
These steps are shown in the image below.