Divide and Conquer

By the end of this lesson, you should be able to:

Solve problems using recursion
Identify problems that has recursive solutions

Important words:

recursion
base case
recursive case
helper function
recursive tree

Introduction

Many computing problems are recursive in structure. With the word recursive we mean that to solve a given problem, they call themselves one or more times to solve a closely related problems. These algorithms in a way follow a divide-and-conquer approach.

Divide and conquer approach breaks the problem into several subproblems that are similar to the original problem but smaller in size. The algorithm then solves this smaller problems and then combines the solutions to create the solution to the original problem. The divide-and-conquer paradigm involves three steps at each level of the recursion:

Divide the problem into a number of smaller problems.
Conquer the smaller problems by solving them recursively and when the problem is small enough, hopefully, it can be solved trivially.
Combine the solutions of the smaller problems into the solution for the original problem.

Summing The Elements of an Array

We will start giving example of divide-and-conquer approach by solving the following problem: summing a list of numbers in an array. Given a list of array, we can sum them by iterating over each element and sum each element to get the final solution. This iterative solution looks as follows.

def sum(array):
    result = 0
    for number in array:
        result += number
    return result

input_array = [4, 3, 2, 1, 7]
print(sum(input_array))

The output is

(C)ases

Another way of solving this problem can be done using a divide-and-conquer approach. In this approach we divide the input array into two parts. The first part consists of a single number while the second part consists of the rest of the numbers. For example, using the input in the above example, we have

[4, 3, 2, 1, 7]

The above input is now divided into two parts:

4 | [3, 2, 1, 7]

This is the divide step. In the conquer step, we recursively solve the second part using the same method. This means that we divide the second part into two parts as follows.

[3, 2, 1, 7]

becomes

3 | [2, 1, 7]

And this continues recursively

[2, 1, 7]

becomes

2 | [1, 7]

and

[1, 7]

becomes

1 | [7]

Now the second part consists of only a single number, i.e. 7. Since the problem is small enough, the solution to the sum problem is simply this number, which is 7. This means that the sum of an array with a single number is just that number. So we can now proceed to the combine step. We will combine the result by adding the number on the left with the sum of the array on the right.

1 | [7] = 1 + 7 = 8

and now we can move up

2 | [1, 7] = 2 + 8 = 10

similarly, we have these two summations

| [2, 1, 7] = 3 + 10 = 13

| [3, 2, 1, 7] = 4 + 13 = 17

(D)esign of Algorithm

Let’s write down the steps on how we solve those particular cases.

Show Pseudocode

Input: Array or list of numbers
Output: the Sum of the array
Steps:
1. if the number of element is one only
    1.1 Return that element as the sum of the array
2. Otherwise,
    2.1 Return the addition of the first element with the sum of the rest of the array

Recursive Basic Structure

In all recursive solutions, we can always identify two cases:

Base Case
Recursive Case

In the algorithm steps above, step 1 is the base case. Base case is usually trivial and easy to solve. Recall that the strategy for this way of divide and conquer is to divide the problem into smaller problems up to the point that the problem becomes trivial. In this example, a trivial problem is to sum an array with only one element. In this case, the sum is just that element.

Step 2 is the recursive case. Notice in step 2.1 we are adding the first element with the sum of the rest of the array. The sum of the rest of the array is the same problem but with one element less. In this way, we have made the problem smaller. It is called recursive because this step calls the function itself with a smaller number of element in the array. How to break down and make the problem smaller will be one of the challenge in creating recursive solutions. Moreover, identifying the base case will also be important. Let’s take a look at some more example in a later section. But for now, we will analyze the computation time.

Computation Time

As you can guess from the iterative solution, this problem takes $O(n)$ time. This means that as the number of input increases, the computation time increases linearly. How do we come about this computation time for recursive solution? One way to do this is to draw the recursion tree.

In a recursion tree, each node represents the cost of a single subproblem somewhere in the set of recursive function invocations. We then have to do two summations. The first sum is to sum all the cost on each level of the tree to obtain a set of cost-per-level. The second sum is to sum all cost-per-level over all levels to obtain the total cost.

To illustrate that, let’s take a look at the example above on summing the elements in an array. Looking at the pseudocode, we see that the program will execute either step 1 or step 2 and not both. We can then make the following observation:

if it is the base case, the computation time is $O(1)$ because it takes constant time to check the case and constant time to return the element of an array.
if it is the recursive case, the computation time is $T(n) = O(1) + T(n-1)$. The constant time comes from the addition operation which is the combine step. On the other hand, this computation time contains $T(n-1)$ due to the recursive call for $n-1$ elements array.

The recursion tree can be drawn as follows.

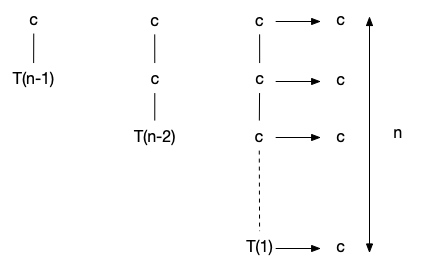
The first figure on the left shows that the computation time for $n$ elements is a constant $c$ plus $T(n-1)$. The second figure in the middle shows the tree when we expland $T(n-1)$. That recursive call is when the input array is $n-1$ elements. The computation time when $n-1$ can be explanded as another $c$ plus $T(n-2)$. We can continue doing this until we are left only with one element, which is shown on the figure on the right with $T(1)$. The tree only has one child on each node and each level has the same cost which shown by the arrow pointing to the right. We can show that there are $n$ levels in the three for $n$ elements of input in the original call.

The cost for each level is a constant $c$ and we have $n$ levels, so the total cost is $cn$, and therefore we can say that the computation time for this recursion is $T(n) = O(n)$.

Factorial Problem

Factorial problem can be defined recursively as follows:

(P)roblem Definition

Taking an integer input $n$, the factorial can be calculated as follows:

\[n! = n \times (n-1)!\]

We also define the factorial of the following input numbers: $0! = 1$ $1! = 1$

Let’s take a look at some particular examples.

(C)ases

Besides those two inputs 0 and 1, we can calculate, for example, the factorial of 5 as follows:

\[5! = 5 \times 4!\]

And we calculate 4 factorial with

\[4! = 4 \times 3!\]

Similarly,

\[3! = 3 \times 2!\]

and

\[2! = 2 \times 1!\]

but we have defined that $1! = 1$. This is the base case. So we can calculate back up.

\[2! = 2 \times 1 = 2\] \[3! = 3 \times 2! = 3 \times 2 = 6\] \[4! = 4 \times 3! = 4 \times 6 = 24\] \[5! = 5 \times 4! = 5 \times 24 = 120\]

Now we can write the steps.

(D)esign of Algorithm

Show Pseudocode

Input: n, an integer
Output: factorial of n, an integer
Steps:
1. if n is equal to 0 or to 1
    1.1 return 1
2. otherwise,
    2.1 return n x factorial of n-1

Notice again here that step 1 is the base case which is trivial. The base case is also the terminating case. Without the base case the recursive solution will not end. So it is important to remember that every recursive solution must have a base case.

Step 2 is the recursive case. In this recursive case, we divide the problem of calculating factorial of $n$ into a smaller problem to calculate only the factorial of $n-1$ and a multiplication. Calculating the factorial of $n-1$ calls the function itself because it is exactly the same problem but with a smaller integer at the input. Let’s discuss the computational time.

Computational Time

The computation time can be calculated as follows:

To check whether it is the base case or not, it takes constant time $O(1)$.
If it is the base case, it returns and exits the function immediately. So the computation time when it is a base case is simply constant time, i.e. $O(1)$.
On the other hand, if it is not a base case, the computation time is $T(n) = O(1) + T(n-1)$. The constant time is the time it takes to multiply $n$ with the factorial of $n-1$. The second term $T(n-1)$ is the computation time to calculate the factorial of $n-1$.

From the above describe, we have the same recursive tree as before.

From here, we can conclude that the computation time is linear, i.e. $T(n) = O(n)$, a function of the input integer.

In the above two examples, summing an array and calculating a factorial, the solutions can be written either using recursion or iteration (such as a for-loop). It is not evident why we need a recursive solution in these two cases. However, there are cases when the iterative solution would be too complicated and its recursive solution is simple and elegent. One example of this is the problem of Tower of Hanoi which we will discuss next.

Tower of Hanoi Problem

Tower of Hanoi is a classic example of when its recursive solution is simple and elegant. The problem is specified as follows.

(P)roblem Definition

Given $n$ disks and three towers, one has to move the $n$ disks from the source tower to the *destination tower using the other *auxilary* tower. See figure below.

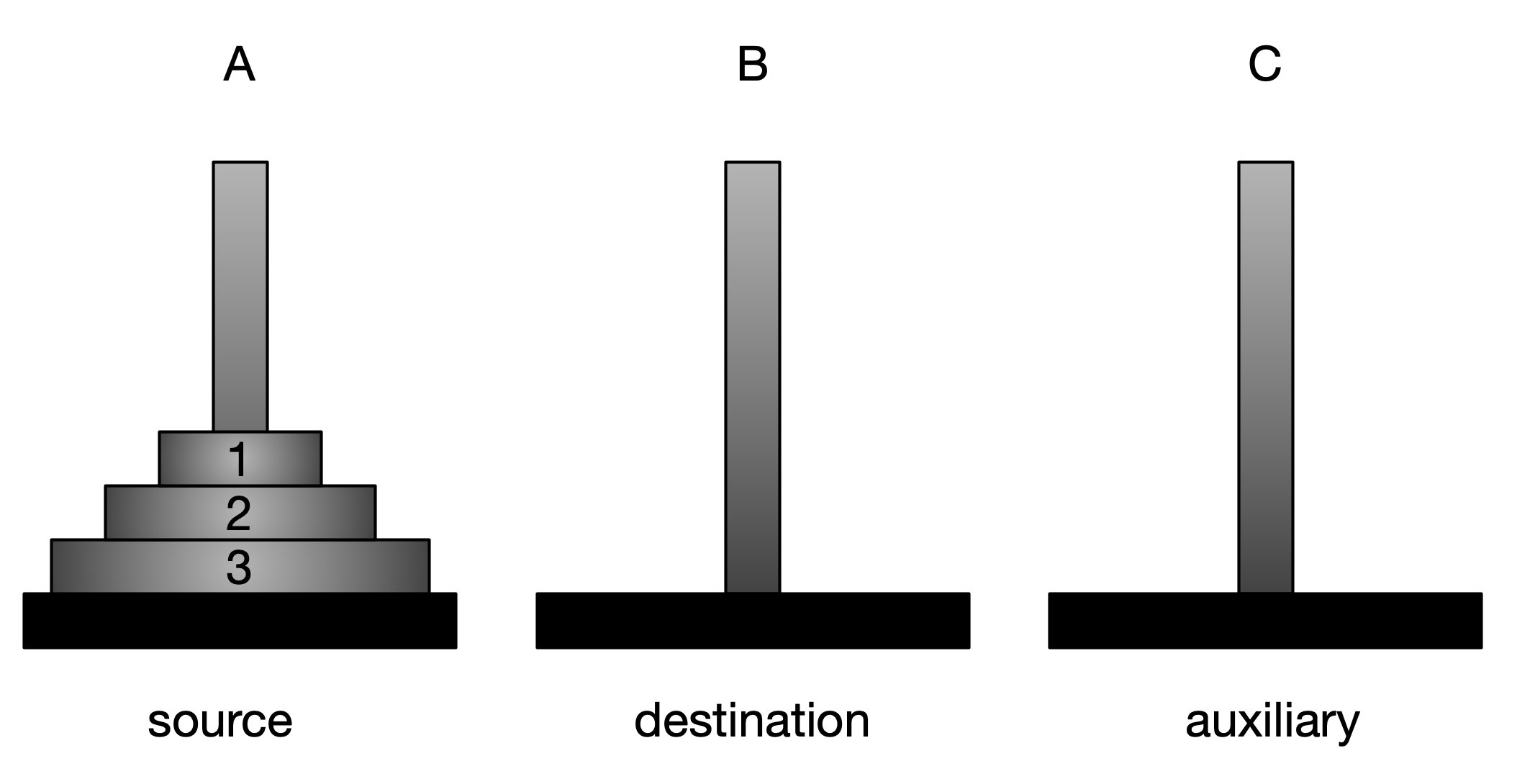
In the above figure, we have three towers A, B, and C. And we have to move $n=3$ disks from tower A to tower B using tower C as the auxiliary tower.

The rules in moving the disks are as follows:

We can only move one disk at a time
A bigger disk cannot be placed on top of a smaller disk

Note that $n$ can be 1 or greater.

(C)ases

Let’s look at some particular cases. Let’s start with a simple case when $n=1$. In this case, to move one disk from A to B is trivial.

Move disk 1 from A to B

and we are done.

How about when $n = 2$. Recall that our source tower is A and the destination tower is B while the auxiliary tower is C. In order to move two disks, we can do the following.

Moving two disks:

Move disk 1 from A (source) to C (auxiliary)
Move disk 2 from A (source) to B (destination)
Move disk 1 from C (auxiliary) to B (destination)

Let’s take a look when $n = 3$. To work this out, you can use the simulation for tower of Hanoi. We will divide this into a few step. The first step is to move the first two disks from A (source) to C (auxiliary). In order to move two disks, we already have the solution as shown above. So we can use the steps above with the difference in the destination and auxiliary towers.

Step 1

Move disk 1 from A (source) to B (destination)
Move disk 2 from A (source) to C (auxiliary)
Move disk 1 from B (destination) to C (auxiliary)

Now we have the first two disks at C (auxiliary). The next step is to move disk 3 from A (source) to B (destination). This consists of only one step.

Step 2

Move disk 3 from A (source) to B (destination)

The last step is to move the two disks from C (auxiliary) to the destination tower B. This again involves a similar three steps with differences in the source and destination towers. The steps to move the two disks to the final destination tower is as follows.

Step 3

Move disk 1 from C (auxiliary) to A (source)
Move disk 2 from C (auxiliary) to B (destination)
Move disk 1 from A (source) to B (destination)

Notice that Step 1 and Step 3 involve the same steps as in Moving two disks. In fact, we can see Step 1 as Moving two disks with tower A as the source and tower C as the destination using tower B as the auxiliary tower. Similarly, we can see Step 3 as moving two disks with tower C as the source and tower B as the destination with tower A as the auxiliary tower. Moreover, the steps in Moving two disks are exactly the same three steps. We first move the top disks to the auxiliary tower, then the bottom disk to the destination tower, and lastly the top disks to the destination tower. In this way, we can use the same steps whenever there are more than 1 disks. In general, we can view this problem for $n$ disks as shown in the figure below.

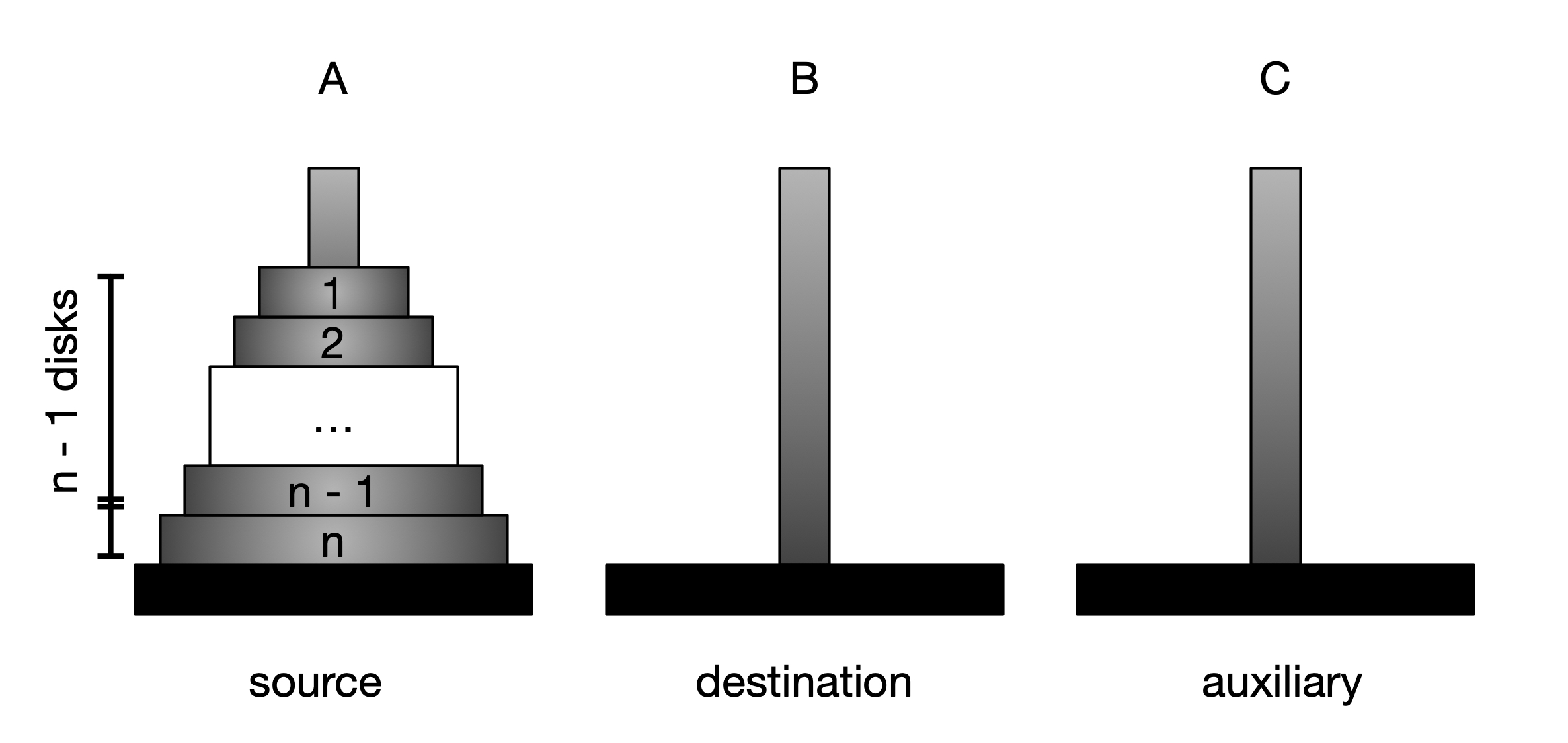
where we divide the disks into two parts:

the first $n-1$ top disks
the last disk $n$

We can then generalize the Tower of Hanoi problem to any number of disks as in the following steps.

(D)esign of Algorithm

Show Pseudocode

Input: 
  - n, number of disks
  - source tower
  - destination tower
  - auxiliary tower
Output:
  - sequence of steps to move n disks from source to destination tower using auxiliary tower
Steps:
1. if n is 1 disk:
    1.1 Move the one disk from source to destination tower
2. otherwise, if n is greater than 1:
    2.1 Move the first n - 1 disks from source to auxiliary tower
    2.2 Move the last disk n from source to destination tower
    2.3 Move the first n - 1 disks from the auxiliary tower to the destination tower

Notice that in the above steps, step 1 is the base case while step 2 is the recursive case. The base case is when the solution is trivial. This is the case when there is only one disk. The solution involves only one step which is to move that one disk from the source to the destination tower. On the other hand, step 2 is the recursive case. In this step, both steps 2.1 and step 2.3 are the recursive steps that reduce the problem smaller to $n-1$ disks. Step 2.2 consists of only a single step.

Looking into these steps and compare it with the examples in the previous steps, we observe that both the steps in moving two disks and the three steps in moving $n=3$ disks fall under the same recursive step 2. Both consist of three general steps 2.1, 2.2, and 2.3.

Computational Time

Now, let’s analyze it’s computational time. Looking into the steps above, we note the following:

it takes $O(1)$ to do the comparison whether it is one disk or more
if it is only one disk, it takes $O(1)$ time to produce the single step and exit the function
otherwise, it takes $T(n-1)$ time for step 2.1, and $O(1)$ for step 2.2, and another $T(n-1)$ for step 2.3

Let’s draw the recursive tree for 3 disks.

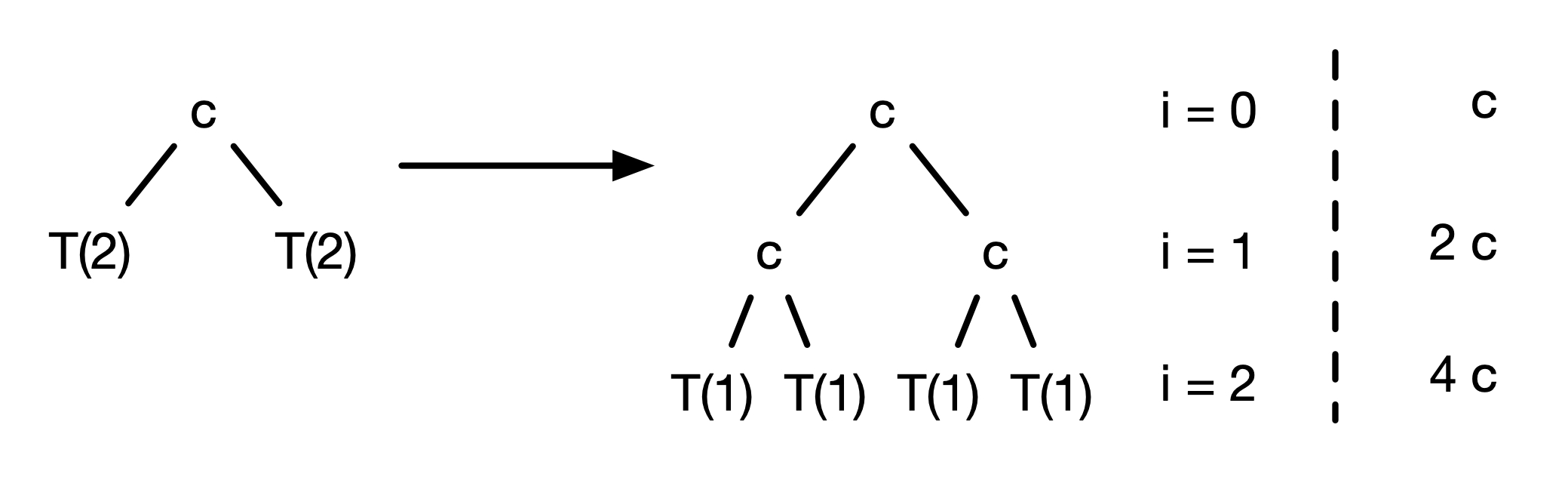
Note that if $n=3$, it takes constant $c$ time and $2 \times T(n-1) = 2 \times T(2)$ computational time. In the recursive steps, each of this $T(2)$ recursive call consists of another constant $c$ time and $2 \times T(1)$ time. The tree stops at $i = n - 1 = 2$ when it reaches the base case as there is only one disk left.

Now we can generalize this to $n$ disks. The recursive tree looks as the one below.

There will be $n$ levels from $i = 0 $ up to $i = n - 1$. Moreover, at each level, the sum total time is $2^i \times c$. If we sum up all the levels, we have the following series:

\[T(n) = \sum_{i = 0}^{n-1} 2^i c = c \sum_{i = 0}^{n-1}2^i\]

Recall that the sum for a Geometric series is given as follows

\[a + ar + a r^2 + \ldots + a r^{n-1} = \frac{a(1-r^n)}{1 - r}\]

where $a$ is the constant of the series and $r$ is the ratio. In our case, $a = c$ and $r = 2$. So we have

\[T(n) = c \sum_{i = 0}^{n-1}2^i = \frac{c(1-2^n)}{1 - 2} = c (2^n -1) = O(2^n)\]

This means that the computational time for the Tower of Hanoi problem is exponential with respect the input. As the number of input increases, the time it takes increases exponentially.

when $n = 1$, it takes 1 step
when $n = 2$, it takes 3 steps
when $n = 3$, it takes 7 steps
when $n = 4$, it takes 15 steps
when $n = 5$, it takes 31 steps

Notice also that in this case $c = 1$ as we can get the number of steps from $2^n - 1$.

PREVIOUSComputation Time

NEXTMerge Sort